Week 2: Input Partitioning & Boundary Value Analysis
The Challenge: Selecting Test Cases
The central problem in testing is that you can't test everything. The set of all possible inputs a program can accept is called the Input Domain. 测试的核心问题是你无法测试所有内容。程序可以接受的所有可能输入的集合称为 输入域。
For example:
- A function
int area(int x, int y)that takes two integers has roughly 264 possible input pairs. 一个函数 'int area(int x, int y)' 接受两个整数,大约有 264 个可能的输入对。 - A search bar that accepts a string has a potentially infinite number of inputs. 接受字符串的搜索栏具有潜在的无限数量的输入。
Testing every single input is impossible. Therefore, we need intelligent techniques to select a small, manageable subset of test cases that are most likely to find faults. This lecture focuses on two such techniques: Input Partitioning and Boundary-Value Analysis. 测试每一个输入是不可能的。因此,我们需要智能技术来选择最有可能发现故障的一小部分、可管理的测试用例子集。本讲座重点介绍两种这样的技术:输入分区和边界值分析。
Input Partitioning & Equivalence Classes (ECs)
Input Partitioning is the process of dividing the massive Input Domain into smaller, manageable chunks called 输入分区是将海量输入域划分为更小的、可管理的块的过程。
Equivalence Classes (ECs).
The core idea is that for any given EC, all the test inputs within that class are "equivalent"—meaning if one of them finds a bug, any other one in that class would likely find the same bug. Therefore, you only need to pick one representative test from each class.
核心思想是,对于任何给定的 EC,该类中的所有测试输入都是“等效的”——这意味着如果其中一个发现错误,该类中的任何其他测试输入都可能发现相同的错误。因此,您只需从每个班级中挑选一项具有代表性的测试。
For ECs to be effective, they must have two properties:
- Coverage: The union of all your ECs must cover the entire input domain 覆盖范围:所有 EC 的并集必须覆盖整个输入域。
- Disjoint: No input can belong to more than one EC 不相交:任何输入都不能属于多个 EC。
The Six Partitioning Guidelines
| # | Guideline | What to Create | Common Bug it Finds | |
|---|---|---|---|---|
| 1 | Ranges | Below range ( | < L), within range (L <= x <= U), and above range (> U). | Off-by-one errors. |
| 2 | Discrete Sets | One EC for each valid item in a set (like an enum), plus one EC for an invalid item. | Forgotten | case labels in a switch statement. |
| 3 | Number of Inputs | If a function expects N inputs, create ECs for | < N, = N, and > N inputs. | Incorrectly handled loop bounds. |
| 4 | Zero-One-Many | Universal for collections. Create ECs for size 0 (empty), size 1, and size > 1. | Errors with empty loops or single-item collections. | |
| 5 | Must Rule | For any rule like "input must be X," create one EC that satisfies the rule and one that violates it. | Missing pre-condition checks. | |
| 6 | Intuition/Experience | Use domain knowledge to identify special cases or common error patterns. | Classic errors specific to an algorithm or domain. |
Building a Test Template Tree (TTT)
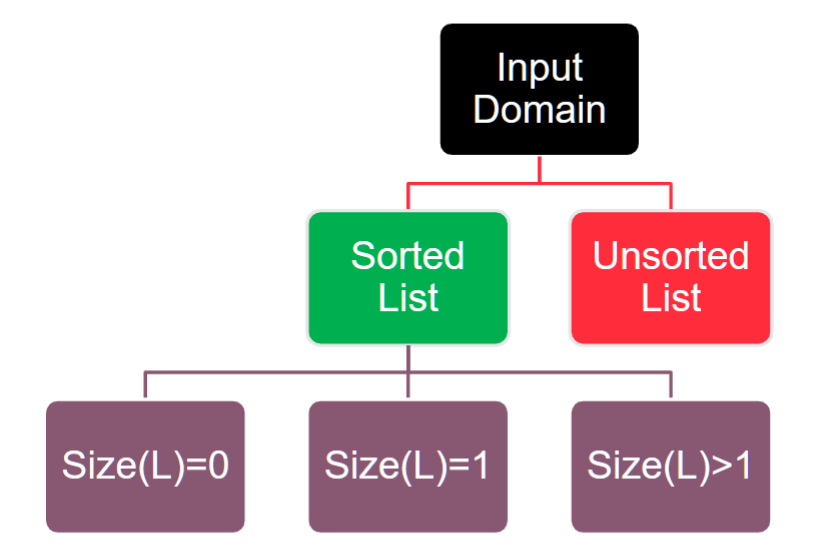
A Test Template Tree (TTT) is a visual, hierarchical method for applying the partitioning guidelines to derive a complete set of ECs. The lecture walks through building a TTT for a binarySearch function. 测试模板树 (TTT) 是一种可视化的分层方法,用于应用分区准则来派生一组完整的 EC。该讲座将介绍如何构建 'binarySearch' 函数的 TTT。
The process involves:
- Starting with a top-level partition based on the specification (e.g., the list must be sorted, so the first partition is "Sorted List" vs. "Unsorted List"). 从基于规范的顶级分区开始(例如,列表必须排序,因此第一个分区是“排序列表”与“未排序列表”)。
- Applying a guideline to a branch to create sub-partitions (e.g., applying the "Zero-One-Many" guideline to the "Sorted List" branch creates nodes for
Size(L)=0,Size(L)=1, andSize(L)>1). 将指南应用于分支以创建子分区(例如,将“零一多”指南应用于“排序列表”分支会创建“Size(L)=0”、“Size(L)=1”和“Size(L)>1”的节点)。 - Continuing this process, applying more guidelines to further partition the inputs (e.g., applying the "Ranges" guideline for the
targetvalue). 继续此过程,应用更多准则来进一步划分输入(例如,对“目标”值应用“范围”准则)。
Each unique path from the root of the tree to a leaf node represents one specific Equivalence Class, which is a combination of all the conditions along that path. 从树的根到叶节点的每条唯一路径都代表一个特定的等价类,它是该路径上所有条件的组合。
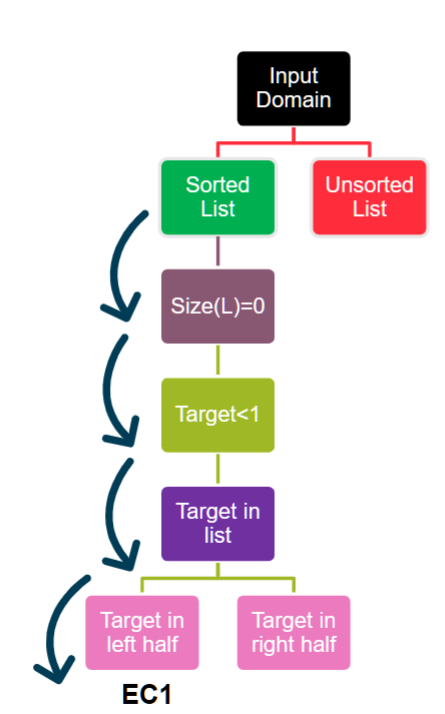
Pruning the TTT
Applying these guidelines can create a "combinatorial explosion" of ECs. Not all of these ECs are actually possible. For example, the path
(Sorted List) & (Size(L)=0) & (target in list) is infeasible because an empty list cannot contain the target. You must analyze each path and prune the ones that are logically impossible. '(Sorted List) & (Size(L)=0) & (target in list)' 是 不可行的,因为空列表不能包含目标。您必须分析每条路径并修剪逻辑上不可能的路径。
Boundary Value Analysis (BVA)
Boundary Value Analysis (BVA) is a technique that complements Input Partitioning. It's based on the observation that errors are most likely to occur at the boundaries between equivalence classes. Consider a function with a condition if (x <= 0). The boundary is at x=0. 边界值分析 (BVA) 是一种补充输入分区的技术。它基于这样一个观察结果,即错误最有可能发生在等价类之间的边界处。 考虑一个条件为“if (x <= 0)”的函数。边界位于“x=0”处。
- The ECs are
x <= 0andx > 0. - A standard EC test might pick
x = -5andx = 10. - But what if the programmer mistakenly wrote
if (x < 0)? The testx = -5would still pass. The testx=10would also pass. However, if you inputx=0, the program will crash with a division-by-zero error. The bug was right on the boundary, and the EC tests missed it.
BVA defines two types of test points to catch these bugs:
- On-Point: A value lying exactly on the boundary (e.g.,
x=0). On-points are the most powerful tests for finding boundary faults. 位于边界_exactly on_的值(例如,'x=0')。点是查找边界故障的最有力测试。 - Off-Point: A value immediately adjacent to the boundary on either side (e.g.,
x=-1andx=1). 紧邻两侧边界的值(例如,'x=-1' 和 'x=1')。
By systematically testing the on-points and off-points for each boundary in your program's input domain, you can significantly increase your chances of finding common off-by-one and boundary shift errors. 通过系统地测试程序输入域中每个边界的开点和偏离点,您可以显着增加发现常见的 off-by-one 和边界移位错误的机会。